LeetCodeの"Magical String"にやたら悩まされたので書いた

Cpp

社内メンバーで LeetCode を解く会をやっていた時、"Magical String" という問題にやたら悩まされたので、反省も兼ねて知見を書いておいた。
Magical String - LeetCode

設問内容

マジックストリング S は '1' と '2' で構成される。
S は '1' と '2' の連続した出現回数を連結したものが出力される。
最初〜いくつかの要素は "1221121221221121122..." のようになる。
これを連続した文字でグループ化すると 1 22 11 2 1 22 1 22 11 2 11 22...... になる。
各グループでの '1' と '2' の出現は 1 2 2 1 1 2 1 2 2 1 2 2...... になる。
これは S 自体であることがわかる。

整数 N を入力し、文字列 S の N 文字から '1' が現れる回数を返してね。
（制約は書いてないが N <= 100000 となっている）

I/O

N = 6 において、マジックストリング S の最初の 6 つの要素は '12211' である。
'1' は 3 つ数えられるので 3 を返す。

6 つの要素と書いてあるのに、5 つまでしか書いてないところが悲しい。

マジックとは

問題を読んでも意味がわからなかったので苦労した。わかるまで読みましょう。
「連続した」と訳した部分は "contiguous occurrences" なので、要するに「隣接して続く」こと。
だから '1' だから 1 回続くとか、 '2' だから 2 回続くとか、'1' や '2' が 3 回以上続くわけではない。

そして、何がマジックでどうやって求めるのかわからなかったけど、ちゃんと読んだらわかった。
隣接して続く文字列 '1' と '2' をグループ化したもの（1, 22, 11, 2, 1, 22, 1, 22, 11, 2, 11, 22）と、グループごとの文字数を並べたもの（1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2,）は、同じ 1221121221221121122 になるという話だった。
これはコーラコスキ数列（Kolakoski sequence）と呼ばれるものらしい。
Kolakoski sequence - Wikipedia

解法

入る文字列は '1' と '2' だけなので、最初の組み合わせを少し考える。

  • 1, 1 (1 が 2 回なので最初は 2 でないと合わない）
  • 2, 1（2 が最初だと 2 回来ないといけないので、次は 2 なはず）
  • 2, 2 (2 回文字が続くので 2, 2, 1, 1 と続くが、1, 1 が合わない）
  • 1, 2 (1, 2, 2 とすることで合う）

マジックストリング、かつ設問の期待値が 1 となる最小の文字列として '122' の 3 文字が確定する。
この問題は、N 文字のマジックストリングから '1' が何回出るかを出力すればいいので、N <= 3 までなら計算しなくていい。
'122' を起点にマジックストリングを導き出していけば良さそう。

しかし '1' と '2' のどっちを出力するかがわからない。
そこで、グループ化した 1, 22, 11, 2, 1, 22, 1, 22, 11, 2, 11, 22 に注目してみる。
すると、 1, 2, 1, 2, 1, 2... のグループが交互に続いているだけなので、奇数のグループは '1' を、偶数のグループは '2' を出力できればいいことがわかる。
グループごとの文字列を何回出力するのかは、グループごとの出力回数をまとめた 1, 2, 2, 1, 1, 2, 1, 2, 2, 1, 2, 2 で考えればいい。
つまり S[i] 回。紛らわしい。

雑な図。
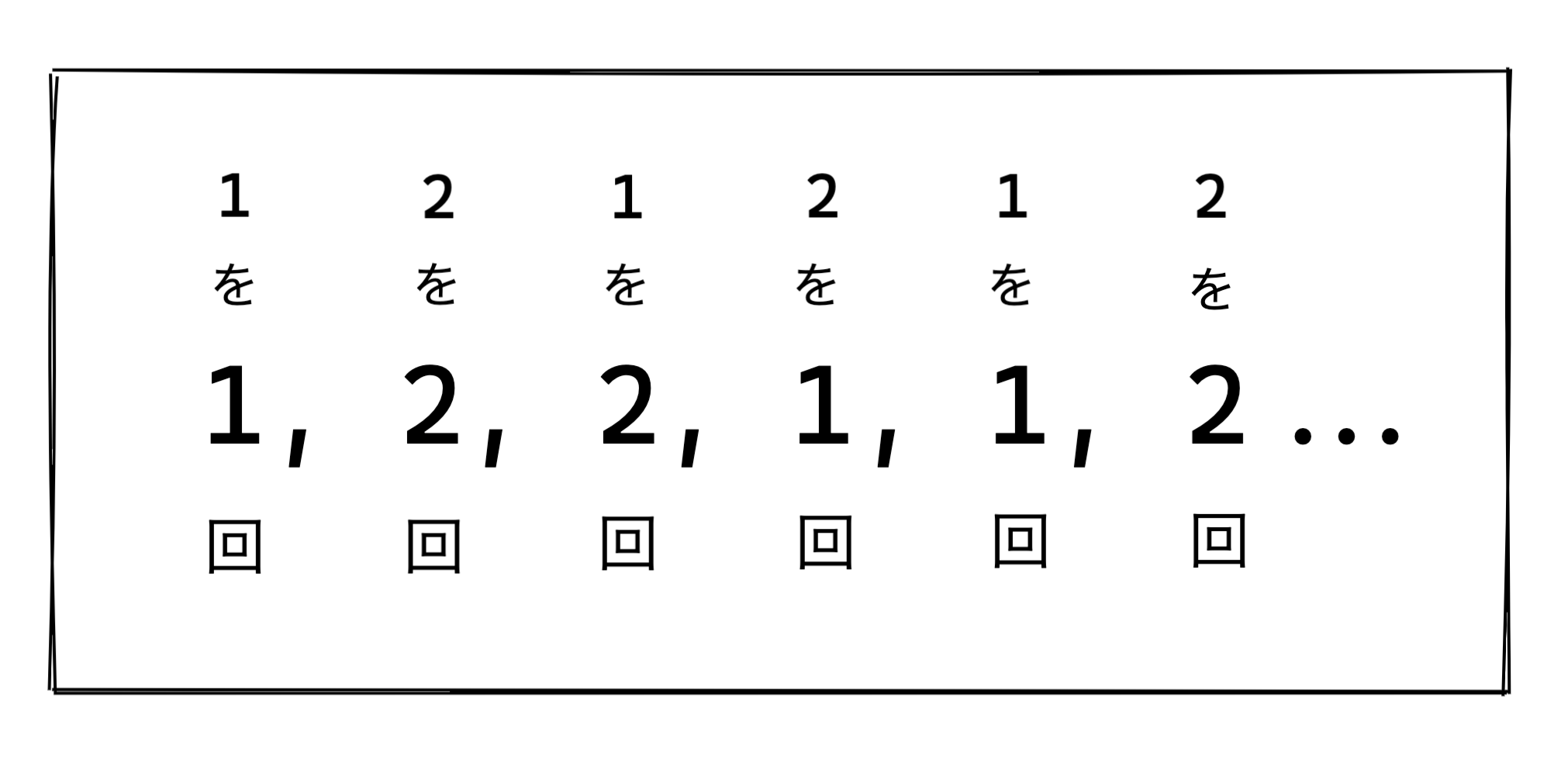
1, 2, 2, 1...という数列を、奇数番の「1」を1回、偶数番の「2」を2回、奇数番の「1」を2回、のように読み替えて出力していく。数字は出力する回数で、奇数偶数は数列のインデックスであることを考えるとわかるかも

こんな感じのを実装する。

main.cpp

#include <algorithm>
#include <string>
using namespace std;

class Solution {
public:
  int magicalString(int n) {
    int res;
    string S = "122";
    int size = S.size();
    if (n <= 0) res = 0;
    else if (n <= 3) res = 1;
    else {
      for (int i = size; i < n; i++) {
        S += string(S[i - 1] - '0', i & 1 ? '1' : '2');
      }
      // N と全体の文字数は一致しないので、S.end()ではない
      res = count(S.begin(), S.begin() + n, '1');
    }
    return res;
  }
};

通ったので完。
他の人の解法を見てると、 '1' か '2' かを S.back() ^ 3 で求めているものもあり、なるほどわからん。

カテゴリー